阻抗型石英晶体微天平,具有适用范围广、获取参数多等优点,但通过阻抗分析方法获取石英晶体谐振频率耗时较长,实时性差。 针对这一问题,对采用最小二乘法进行二次拟合的计算过程进行了深入的分析,对其中的关键步骤进行了改进,提出了一种适用于石英晶体谐振频率测量的快速检测算法,通过对测得数据的坐标系进行调整,降低了拟合过程中的数据运算量。 经实验验证,与传统拟合算法相比,该算法计算谐振频率的效率提升4倍,并且得到了更高的计算精度,具有很高的实用价值。
The impedance analysis quartz crystal microbalance has many advantages such as wide application range and more parameters, but the resonance frequency of the quartz crystal obtained by the impedance analysis method takes a long time and has poor real-time performance. In response to this problem, we analyzed the process of data fitting when using the least squares method and proposed a fast detection method for quartz crystal resonant frequency measurement. By adjusting the data coordinate system, the calculation time used for the fitting process reduced obviously. The new method was verified by experiments, compared with the traditional least squares method, the efficiency of the algorithm for calculating the resonant frequency was improved by four times, and the calculation accuracy was higher. It means the new method has high practical value.
石英晶体微天平(Quartz Crystal Microbalance,QCM)是一款非常灵敏的质量感测设备,它能够实时地测量石英晶体表明极微小的质量变化。 其灵敏度可达纳克级,这意味着它能够实现相当于单分子层的物质检测。 QCM所具有的高灵敏度以及可实时测量的特点,使它在众多领域成为一种极具吸引力的技术。
在1880年,Lippman提出了“反压电效应”并经Curie兄弟进行了实验验证,后经柏林工业大学物理研究所Guenter Sauerbrey[1]推导出Sauerbrey公式奠定了QCM作为传感器应用的基础。 QCM的主要原理是利用石英晶体的压电效应,将石英晶体表面被测物质的质量变化转换为石英晶体的谐振频率变化。 Kanazawa与Bruckenstein[2]发现了振荡频率与溶液的粘弹性和密度成线性关系。 Rodahl等[3,4,5,6]提出了耗散因子的概念,使QCM可以通过耗散因子的检测对吸附在晶体表面物质的粘弹性与厚度进行测量,从而进一步拓宽了QCM的应用范围。 目前,QCM已经在物理、化学[7]、生物及医学[8]领域被广泛应用[9]。
随着各学科交流与技术的不断进步,科研人员将仪器从最初的常规测量发展到流动型QCM、耗散型QCM、阵列型QCM与阻抗型QCM等多种新型原位的分析仪器。 阻抗型QCM,采用阻抗分析的方式,不仅可以获得石英晶体的谐振频率,还可以同时获得耗散因子、等效电阻等参数,与传统的振荡电路型仪器相比,具有适用范围广、测量参数多等优点。 但采用阻抗分析的方式进行谐振频率测量,需要进行一定范围的频率扫描,对所得到的数据进行拟合运算,一次测量所需时间较长,使得仪器的实时性较低。 为解决这一问题,本文对阻抗分析法中石英晶体谐振频率的求解过程进行了改进,提出了一种快速且精确的优化方法,并进行了实际测试验证。
自行研制的耗散型电化学QCM(Electrochemical Quartz Crystal Microbalance with Dissipation Monitoring,EQCM-D),石英晶体为北京晨晶电子有限公司购买的石英裸片,通过EMSCD050型高真空溅射镀膜仪(德国Leica公司)真空溅射制的镀金石英晶片。 硬件控制器采用STM32F407IGT6型单片机(意法半导体)[10]。
浓硫酸、硫酸铜、氯化钠均为分析纯试剂(北京试剂厂)。 实验用水为经过 Milli-Q 系统制备的超纯水(阻抗>18.2 MΩ·cm)。
石英晶体等效电路可用图1A所示的巴特沃斯(Butterworth-van Dyke,BVD)等效电路来模拟,石英晶体表面物质特性发生变化时,一般认为是BVD模型中等效参数的数值在发生变化。 其中静态电容 C0是由石英晶体金属电极及引线电容构成的, Ls和 Cs分别代表石英晶体的惯性和弹性, Rs代表晶体振动时因摩擦而造成的损耗。 通常 C0很小,在几pF到几十pF, C0对串联谐振回路的影响可由硬件电路补偿抵消,因此这里不用考虑 C0的影响, Rs可以在10~103 Ω范围。
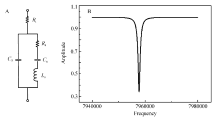 | 图1 石英晶体巴特沃斯等效模型(A)及7.955 MHz石英晶体幅频特性(B)Fig.1 Quartz crystal Butterworth-van dyke mode(A) and amplitude frequency characteristics of 7.955 MHz quartz crystal(B) |
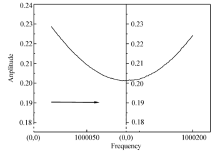
通过一个定值电阻 Ri对石英晶体施加激励(频率扫描),得到电压节点 V0的幅频特性如图1B所示,当激励达到串联谐振频率 fs时,串联谐振回路( RS、 CS、 LS)呈现纯阻性,此时石英晶体的阻抗最小,电压 V0的幅值最小;当激励信号频率远离串联谐振频率时石英晶体阻抗逐渐变大,响应信号的幅值也即逐渐变大。 根据这一性质,通过改变激励信号的频率,测量响应信号的变化,可得到响应点电压 V0的幅频特性曲线。 因为最终频率以1 Hz间隔步进扫频时在谐振频率点附近各幅值比较接近,以幅值最低点来确定谐振频率点会出现很大的干扰,通过实际测量发现在谐振频率附近幅频特性曲线类似二次函数曲线形式。
在扫描频率 f( Xi)刺激下可以得到相应节点 V0的值 Yi,通过最小二乘法进行数据分析,采用代数多项式进行曲线拟合,一般情况下二次拟合与三次拟合得到的结果相似,为减小系统额外开销一般选用二次拟合即可,最终可以寻求到近似函数 f( x)描述数据变化规律。
其原理为设定数据序列为( Xi, Yi)( i=1,2…… n),设拟合的函数形式为式(1):
式中, a0、 a1、 a2进行求解。 使得测量的离散数据尽量靠近这条曲线,设拟合函数的均方误差为式(2):
由多元函数的极值原理,选取 a0、 a1、 a2使得这个函数取极小值,于是推导出式(3):
对式(3)进行整理得到式(4):
式中, Xi、 Yi分别为扫描频率和对应的幅值大小。 求解式(4),即可求出拟合的二次函数各项系数。 由前文可知当激励达到串联谐振频率 fs时,串联谐振回路( RS、 CS、 LS)呈现纯阻性,此时石英晶体的阻抗最小,即幅值最低点。 从而确定谐振频率点为(- a1 /2 a2,(4 a2 a0-
由于QCM的宽频自适应特性,在仪器实际工作时,需要不断的变化扫描频率范围来得到振幅频率特性曲线。 通过仪器可以测量到多组离散的频率与幅值点,如果重新定义坐标轴,如图2所示曲线的形状不会改变,改变的只是横坐标偏移量,在新坐标系下拟合后得到的结果再加上原来的偏移量就是原坐标系下的结果。 具体实现方法如下:
1)首先在原坐标系中寻找振幅最小值点( x1, y1);2)取点( x1, y1)左右各 m个点,共2 m+1个点用于拟合计算;3)重新选取坐标系,此时原坐标系下点( x1, y1)变为(0, y1),在式(4)中,坐标 X的一次项和三次项将变为奇函数,因此其累加和均为0。 式(4)变为如下形式:
4)对非齐次线性方程组(5)进行求解,得到二次函数各项系数 a2, a1, a0 ,最终求得实际谐振频率 f=- a1 /2 a2+ X1。
对非齐次线性方程组(5)进行求解过程中计算过程还可进行简化,因为 X的一次项是奇对称, X的平方项是偶对称,因此
常规QCM扫频的检测范围一般在1~10 MHz,部分仪器可以施加 n=1,3,5… n奇数倍的信号,最高可达70 MHz[11],测量数量级为107~108,分辨率为0.02~1 Hz。 并且由于其良好的性质往往与电化学联用进行反应过程的原位分析。 从而要求QCM硬件电路具有一定的实时性,即需要单片机具有良好的处理速度用于完成数据采集与传输。 由于QCM的测量机理,在实际寻找谐振频率时通过常规二次拟合会有一定的局限性,主要在于谐振频率有效位较多,通过拟合算法计算后谐振频率精度不够;基于阻抗法需要大量离散的数据进行拟合,若拟合时间较长则仪器的测量实时性较差。
QCM作为高精密仪器,其质量检测由Sauerbrey式(6)可知,质量的变化(Δ m)与频率(Δ f)在一定条件下呈现线性关系(式中, f0为初始状态下石英晶体谐振频率, ρq为石英晶体密度2.648 g/cm3, μq为石英晶体剪切模量2.947×1011 g/(cm·s2), Cf为石英晶体的灵敏因子),以9 MHz晶体为例,每5.4 ng/cm2就会产生1 Hz的频率变化(Δ f)。 从中可以看出,谐振频率的精度对仪器的测量结果具有很大的影响。
在数值计算中Float类型最多有7位有效数字,绝对精度只能保证6位。 Double类型最多有16位的有效数字,能保证的绝对精度有15位。 而在数量级如此大的计算中,数据有效位数要求大于自身类型能保证的位数,否则难免在计算中会出现精度损失,造成最终谐振频率计算出现不同程度的偏差。图3比较了通过常规最小二乘法在以Double和Float类型进行计算时,在不同谐振频率下谐振频率计算误差,在计算机(PC)上进行了数据的模拟结果。 选取1001个离散的数据点,以1000为步进,进行模拟计算。将计算结果与真实数据的顶点位置做差,记为 X的偏移。 随着频率的增大,不论是Double类型还是Float类型谐振频率偏移逐渐变大。 造成这一现象的原因是计算数量级远超出该数据类型支持的有效精度,导致了数据的溢出。 分别查看Float在0~8 kHz,其平均偏移已经在2986.899781 Hz,Double在90~140 kHz的平均偏移已经达到了3.2922214 Hz,在140~200 kHz平均偏移达到27.39254 Hz,在频率未达到1 MHz的时候,随着频率的增加误差也随之增大。 从而可以得出结论,常规的最小二乘法在测量范围与测量精度上无法满足QCM的测量需求。
 | 图3 二次函数拟合对于谐振频率计算的偏移Fig.3 The deviation of quadratic function fitting A.Float type; B.Double type for the offset of resonant frequency |
若通过高精度算法完成最小二乘法的运行过程,可以具有良好的精度范围,但也造成了额外的系统空间与运行时间。 高精度算法的本质为通过开辟一定的内存空间用于存储数据,一般通过一个数组或自定义的数据结构存储数据。 虽然精度可以根据开辟空间的大小进行保证,但在计算时需要对整体进行遍历还增加了其它的系统开销。
通过在PC机上选用开源的库MPIR(Multiple Precision Integers and Rationals Library)作为高精度算法与改进后最小二乘法算法进行模拟对比测试。 分别在0~10 MHz,每间隔100 Hz执行一次算法,共执行100000次,最终取平均运行时间。 其中高精度算法平均运行时间为435.233 μs,改进后二次函数算法为1.902 μs。 二者精度均可以保证小数位后5位,充分满足仪器对频率的需求。 但从运行时间角度上来看,改进后的二次拟合函数算法具有速度上的绝对的优势。目前可用的高精度算法库仅针对计算机适用,高精度算法库在单片机上使用需要进行大量的移植与后期维护工作。
配制1 mol/L H2SO4和10 mmol/L CuSO4混合溶液,在混合溶液中进行QCM与循环伏安法联用测量,如图4A所示,对应的频率变化与电量关系如图4B,为进行精细分析,还原过程放大如图4C,氧化过程如图4E,对应的频率变化与电量关系图分别如图4D和图4F。 随着电势从0.3 V扫至-0.3 V,溶液中的铜离子先还原沉积,再反向扫回0.3 V,相应沉积的铜再氧化溶解,频率变化的起点和终点可完全重合说明沉积的铜可以完全溶解,电极状态可以完全恢复。
式(6)与法拉第公式联合可推出 M/n= (-Δ f /Δ Q)· F/Cf,式中, M为摩尔质量, n为得失电子数, F为法拉第常数, Q为电量,通过该公式可以表达每摩尔电子转移引发质量变化。 对硫酸铜的整体、氧化、还原过程分别进行计算 M/n,其结果如图4B、4D和4F,分别对各部分进行计算,各过程的 M/n为分别为32.00、34.08和28.23 g/mol,根据反应溶液可知主体反应为Cu与Cu2+沉积与溶解过程,铜的 M/n的理论值为31.75 g/mol,与理论值基本一致,该实验从电化学联用的角度表征了仪器的谐振频率计算准确性,实际测量的表观 M/n,特别是氧化溶解过程测量的表观 M/n偏离理论值较大,反映了还原沉积过程近乎以均匀的速度进行,而氧化溶解过程则复杂的多,会受到电极表面状态、双电层的充放电和离子的吸附等的影响[12]。
本文提出了一种基于最小二乘法的二次函数曲线拟合石英晶体微天平(QCM)谐振频率检测方法,并给出了谐振频率求解过程。 与传统的最小二乘法曲线拟合求解相比,经过优化后的二次函数拟合方法在仅支持硬件单精度浮点型运算的STM32单片机上得到了很好的应用,仅仅使用单精度浮点型便可完成计算求解,且谐振频率计算精度与频率数量级无关,经在STM32F407IGT6上实际测试,选取1001个点进行二次拟合,常规方法需要48 μs完成拟合,改进后的方法只需要12 μs就可完成拟合,效率提高为4倍。 经实际测试,该方法简单有效,在QCM谐振频率测量中得到了很好的应用。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|