小角X射线散射技术的绝对散射强度校正

摘要
关键词
Abstract
Keyword
1 实验仪器
2 校正原理与步骤
2.1 原理
Figure1
2.2 验证
3 应用实例
3.1 聚甲基丙烯酸甲酯(PMMA)乳液
Figure2
Figure3
3.2 高密度聚乙烯
Figure4
4 结论
参考文献

引用本文

陈冉, 门永锋. 小角X射线散射技术的绝对散射强度校正[J]. 应用化学, 33(7): 774-779
CHEN Ran, MEN Yongfeng. Calibration of Absolute Scattering Intensity in Small-angle X-Ray Scattering[J]. Chinese Journal of Applied Chemistry, 33(7): 774-779 复制到剪切板

Permissions

本文属于开放获取期刊，遵循CCAL协议，使用请注明出处。

小角X射线散射技术的绝对散射强度校正

陈冉^a,^b, 门永锋^a,^*

^a 中国科学院长春应用化学研究所,高分子物理与化学国家重点实验室长春 130022

^b 中国科学院大学北京 100049

通讯联系人:门永锋,研究员; Tel:0431-85262907; Fax:0431-85262954; E-mail:men@ciac.ac.cn; 研究方向:高分子物理

收稿日期:2015-12-28 修回日期:2016-03-02 接受日期:2016-04-18

基金:国家自然科学基金资助项目(21134006);

摘要

小角X射线散射绝对强度的校正对获得样品微观结构定量参数非常重要。本文描述了一种通过对探测器直接测量入射光束的强度进行校正的方法。其适用性利用标准样品(水)的绝对散射强度标定进行了证实。将此方法应用到聚甲基丙烯酸甲酯乳液和高密度聚乙烯上,得到了相应散射体的体积分数和比表面积。 PMMA的体积分数与通过密度算得的结果很接近。淬火的高密度聚乙烯的比表面积比缓慢降温的大。

关键词: 校正; 绝对强度; 小角X射线散射

中图分类号:O631 文献标志码:A 文章编号:1000-0518(2016)07-0774-06

Calibration of Absolute Scattering Intensity in Small-angle X-Ray Scattering

CHEN Ran^a,^b, MEN Yongfeng^a

^a State Key Laboratory of Polymer Physics and Chemistry,Changchun Institute of Applied Chemistry,Chinese Academy of Sciences,Changchun 130022,China

^b University of Chinese Academy of Science,Beijing 130049,China

Corresponding author:MEN Yongfeng, professor; Tel:0431-85262907; Fax:0431-85262954; E-mail:men@ciac.ac.cn; Research interests:polymer physics

Received:2015-12-28 Revised:2016-03-02 Accepted:2016-04-18

Fund:Supported by the National Natural Science Foundation of China(No.21134006)

Abstract

Absolute calibration of small-angle X-ray scattering data is necessary for determining quantitative parameters of microstructure of the samples. This work details the absolute calibration method by the measurement of incident beam directly with Pilatus detector. Absolute calibration of standard sample(water) was carried out to verify this method. Application of this method to a poly(methyl methacrylate) colloidal dispersion and a high density polyethylene were performed to obtain the volume fraction and specific surface of scatters. The volume fraction of polymethylmethacrylate(PMMA) is close to the result calculated by density. The specific surface of quenched high density polyethylene is larger than slow cooled sample.

Keyword: calibration; absolute intensity; small-angle X-ray scattering

Show Figures

小角X射线散射技术中的实测试样散射强度仅仅是相对强度,与实验条件和样品尺寸(如厚度)等有关。相对强度只能用来计算散射体的几何参数,如溶液中高分子的旋转半径、粒径尺寸和片层结构中的长周期等。绝对强度是散射光强与入射光强的比值,也称为单位体积微分散射截面,与光散射中瑞利比(Rayleigh ratio)相似。它只与样品本身的性质有关,与测试仪器、曝光时间、样品尺寸等外部条件都无关。绝对强度用来计算与质量密度有关的参数,如相对分子质量^[1,2]和电子密度差^[3]等。小角X射线散射技术在过去得到广泛应用,然而普遍使用相对强度,只有很少的实验进行绝对强度的校正。原因是入射光强和散射光强相差几个数量级,精确的测量入射光强有一定的难度(光强过大,易将探测器损坏),这给绝对强度的校正造成了障碍。

目前绝对强度的校正方法有两种:第1种称为衰减法或直接法,是用不同厚度的吸收箔^[4,5,6](如Ni片等)或者特殊机械装置(如旋转圆片^[7]和移动狭缝^[8]等)来衰减入射光强,使之达到可准确测量的范围,然后外推出入射光强。第2种称为间接法,即标样法,是用已知绝对强度的样品,如水^[2,9]、聚乙烯^{[10,11,12,13,14]}、二氧化硅悬浮液^[9,15,16]、玻璃碳^[9,16]和金溶胶^[1,17]等,作为标准样品,用与研究样品相同的测试条件测试标准样品的散射强度,将研究试样的相对散射强度转化成绝对散射强度。在衰减法精度不高、装置(旋转圆片和移动狭缝等)较难获得的情况下,标样法是个不错的选择。但是标样法比较繁琐,因为标样的测试需要与测试样品的条件完全相同。这对于散射能力较弱的水来说,更是费时。在本工作中,我们主要针对法国Xenocs SA公司的Xeuss系统的小角X射线散射仪进行绝对强度的校正。它的特点是实验条件多变,标样法更显得效率低。但是由于先进的半导体Pilatus探测器可以直接测量入射光强,这给绝对强度的校正带来希望。我们主要介绍了绝对强度校正的理论,以及关于对Xeuss系统的小角X射线散射仪校正的详细细节,并给出了应用实例。

1 实验仪器

改进型的法国Xenocs SA公司的Xeuss系统的小角X射线散射仪(用于校正)。这个系统装有多重聚焦的Cu Kα X射线源(GeniX^3D Cu ULD),工作电压为50 kV,工作电流为0.6 mA,产生的X射线的波长为0.154 nm,X射线束通过两个相距2400 mm 的无散射狭缝准直。通过调节两个狭缝的大小决定最后入射光斑的尺寸,散射数据通过半导体探测器(Pilatus 100 K,DECTRIS,Swiss)记录,探测器线性记录的界限少于400000 counts/(s·pixel)。像素的大小为172 μm×172 μm。入射光束挡板(beam stop)直径为5 mm。样品到探测器的距离也是可调节的,能实现从小角到超小角的测试^[18]。

2 校正原理与步骤

2.1 原理

微分散射截面的定义^[16]是单位时间单位立体角被散射的光强与入射光强(counts/(cm²·s))的比值(单位是cm²)。对样品的体积作归一化,单位体积微分散射截面的单位是cm^-1。基于以上的定义,我们可以得到单位体积微分散射截面与测量的相对强度 I( q) (counts/s)的关系:

$\begin{matrix} I (q) = \frac{I_{0}}{A_{i}} A_{s} d T_{s} \frac{dΣ}{dΩ} ΔΩt \end{matrix}$ (1)

式中, I₀是入射光强(counts/s), A_i是入射光束在样品位置处的照射面积, A_s是样品被光束照到的面积, d是样品的厚度, T_s是样品的透射率, $\begin{matrix} \frac{dΣ}{dΩ} \end{matrix}$ 是样品的单位体积微分散射截面, t是曝光时间,Δ Ω是探测器上一个像素所夹的立体角。其中立体角的定义^[14]是:

$\begin{matrix} ΔΩ = \frac{p_{1} p_{2} L_{0} / L_{p}}{L_{p}^{2}} \end{matrix}$ (2)

式中, p₁和 p₂是一个像素在水平和竖直方向上的大小, L₀是样品到探测器的距离, L_p是样品到每个像素的距离。

如果样品足够大,入射光束在样品处能全部照到样品上,那么 A_i= A_s。则样品的单位体积微分散射截面是:

$\begin{matrix} \frac{dΣ}{dΩ} = \frac{I (q)}{I_{0} d T_{s} t} \frac{L_{p}^{3}}{p_{1} p_{2} L_{0}} \end{matrix}$ (3)

此式中 I( q)是扣除背底后的强度。在扣除背底时,要注意样品和背底的透射率之差。所以

$\begin{matrix} I (q) = I_{s} (q) - I_{bg} (q) \frac{T_{s}}{T_{bg}} \end{matrix}$ (4)

式中, I_s( q)和 I_bg( q)是测量的样品和背底的相对强度, T_bg是背底的透射率。将此式代入式(3)中,可得最终的单位体积微分散射截面表达式:

$\begin{matrix} \frac{dΣ}{dΩ} = \frac{(I_{s} (q) / T_{s} - I_{bg} (q) / T_{bg})}{I_{0} dt} \frac{L_{p}^{3}}{p_{1} p_{2} L_{0}} \end{matrix}$ (5)

进行绝对强度校正,需注意以下细节:

1)入射光强的测量。入射光强可通过Pilatus探测器直接测量。不放样品,移开入射光束挡板,曝光0.1 s,记录的全部光子数的10倍作为入射光强(可选择其它曝光时间,但是保证在探测器的线性界限之内)。为保证测量的准确性,探测器在开始曝光1 s后开始记录。为了进一步减少光强变化带来的误差,可以在样品和背底曝光前后分别进行两次入射光强的测量。

2)样品透射率的测量。分别测量样品和背底的入射光强,两者比值即为样品透射率。

3)如果样品的散射非常弱(比如水),并且曝光时间比较长,需要进行探测器暗流校正。暗流指没有光子到达探测器,探测器也会记录到的电子流。校正方法是在光源关闭的状态下,用探测器记录与样品曝光相同时间的光子,作为探测器的暗流 I_dark( q)。在透射率的校正之前,样品测试和背底均需要扣除暗流即:

$\begin{matrix} I (q) = [I_{s} (q) - I_{dark} (q)] - [I_{bg} (q) - I_{dark} (q)] \frac{T_{s}}{T_{bg}} \end{matrix}$ (6)

根据校正的绝对强度可以精确计算散射体系的结构参数。如根据Porod方法,两相体系的比表面积 S/V可由下式得到:

$\begin{matrix} \frac{S}{V} = π φ_{A} φ_{B} \frac{k_{p}}{Q_{1}} \end{matrix}$ (7)

式中, φ_A和 φ_B分别为两相的体积分数, k_P为Porod常数, Q₁是积分不变量除以4π:

$\begin{matrix} Q_{1} = \int_{0}^{\infty} \frac{dΣ}{dΩ} (q) q^{2} dq = 2 π^{2} I_{e} (ρ_{A} - ρ_{B})^{2} φ_{A} φ_{B} \end{matrix}$ (8)

式中, ρ_A和 ρ_B分别为两相的电子密度, I_e是一个电子的散射强度:

$\begin{matrix} I_{e} = r_{e}^{2} \frac{1 + co s^{2} 2 θ}{2} = 7.90 \times 10^{- 26} \times \frac{1 + co s^{2} 2 θ}{2} \end{matrix}$ (9)

式中, r_e为经典电子半径,大小为2.818×10^-13 cm。在小角范围内极化因子约等于1。

Porod常数 k_p可由Porod定律得到。对于界限清晰的理想两相体系,在散射曲线的散射角较大的区域,其强度服从:

$\begin{matrix} li \underset{q \to \infty}{m} \frac{dΣ}{dΩ} (q) q^{4} = kp \end{matrix}$ (10)

Porod定律只在两相界面清晰时成立。如果体系中两相界面模糊,ln $\begin{matrix} \frac{dΣ}{dΩ} \end{matrix}$ ( q) q⁴ -q²曲线随着 q的增大而减小,即出现负偏离。对这种现象需要进行负偏离修正,

$\begin{matrix} li \underset{q \to \infty}{m} \frac{dΣ}{dΩ} (q) q^{4} = k_{p} \exp (- 4 π^{2} σ^{2} q^{2}) \end{matrix}$ (11)

式中, σ是与两相间过渡层厚度有关的参数。对式(11)两边取对数,可得:

$\begin{matrix} \ln (\frac{dΣ}{dΩ} (q) q^{4}) = \ln (k_{p}) - 4 π^{2} σ^{2} q^{2} \end{matrix}$ (12)

线性拟合ln $\begin{matrix} \frac{dΣ}{dΩ} \end{matrix}$ ( q) q⁴ -q²曲线尾部,由截距求得Porod常数 k_p。

Figure Option
View Download New Window Download As Powerpoint Slide

图1 ( A)空容器、装满水的容器和扣除空容器的水自身的散射曲线,空容器的散射已经经过透射率的校正;( B)水的绝对强度散射曲线以及相应的最小二乘法拟合,拟合结果是1.652×10^-2 cm^-1Fig.1 ( A)Scattering curves of container, the container filled with water and water alone after subtraction of the empty container. The scattering from the empty container has been corrected for transmission; ( B)The absolute scattering curves of water alone and the corresponding fit by least square method. The fit result is 1.652×10^-2 cm^-1

如果两相中存在畸变及热密度起伏,ln $\begin{matrix} \frac{dΣ}{dΩ} \end{matrix}$ ( q) q⁴ -q²曲线随着 q的增大而增大,即出现正偏离。对这种现象需要进行正偏离修正:

$\begin{matrix} \lim_{q \to \infty} \frac{dΣ}{dΩ} (q) q^{4} = kpexp (4 π^{2} σ^{2} q^{2}) \end{matrix}$ (13)

对此式两边去对数,可得:

$\begin{matrix} \ln (Σ (q) q^{4}) = \ln (kp) + 4 π^{2} σ^{2} q^{2} \end{matrix}$ (14)

线性拟合ln $\begin{matrix} \frac{dΣ}{dΩ} \end{matrix}$ ( q) q⁴ -q²曲线尾部,由截距求得Porod常数 k_p。

如果出现Porod规律的正偏离或者负偏离现象,在计算积分不变量时,要排除由于界面模糊或者畸变及热密度起伏所引起的散射,即:

$\begin{matrix} {\frac{dΣ}{dΩ}}_{true} (q) q^{4} = \exp (\ln (\frac{dΣ}{dΩ} (q) q^{4} \pm 4 π^{2} σ^{2} q^{2})) \end{matrix}$ (15)

2.2 验证

水的绝对强度已知,故采用以上方法进行水的绝对强度的校正来验证其可行性。选用水的优点在于水的散射强度为常数,与散射角无关,仅与等温压缩率有关。缺点在于水的散射很弱,曝光时间很长。

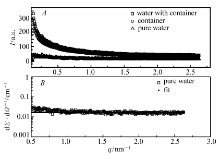
室温(23 ℃)分别测试水、背底和暗流各20 h。样品到探测器的距离为1067 mm。图1 A展示了水及容器、容器和水本身的相对强度散射曲线,其中容器的散射曲线已经过透射率的校正。采用以上方法对水的散射作绝对强度的校正,结果见图1 B。对水的绝对强度作最小二乘法拟合,得到的结果是1.652×10^-2 cm^-1。该结果与水的理论散射强度(1.655×10^-2 cm^-1)在误差范围内相符合,因而证明上述校正方法可行。

3 应用实例

3.1 聚甲基丙烯酸甲酯(PMMA)乳液

我们测试了固含量为8.2%的PMMA乳液(体积分数约为7.0%,是比较理想的两相体系),PMMA为无定形态,密度为1.18 g/cm³,相应的电子密度为390.2 nm^-3。溶剂为水,密度为1.00 g/cm³,相应的电子密度为334.3 nm^-3,曝光时间为2 h,样品到探测器的距离为6498 mm。图2 A为PMMA乳液的绝对散射强度曲线,其Porod曲线及线性拟合曲线,如图2 B所示。由图2 B可知,Porod曲线有正偏离现象,原因是水的热密度起伏造成的^[19]。线性拟合结果:斜率为13.68,截距为-5.56。求得相应的Porod常数 k_P为3.80×10^-3 cm^-1·nm^-4。用式(8)计算积分不变量 Q₁为0.26 cm^-1·nm^-3。已知 Q₁可求得两相的体积分数分别为93.6%和6.4%。由式(7)算的比表面积 S/V为2.67×10⁴ cm^-1。

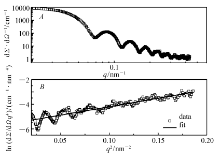	Figure Option View Download New Window Download As Powerpoint Slide
	图2 固含量为8.20%的PMMA乳液的绝对强度散射曲线( A)及相应的Porod曲线( B)Fig.2 The absolute scattering curves of PMMA colloidal dispersion with solid content of 8.20%( A) and the corresponding Porod plot( B)

我们对PMMA的尺寸分布作拟合,假设PMMA为球形状,尺寸分布符合高斯分布。具有高斯分布尺寸分布的球的散射强度公式为:

$\begin{matrix} I (q, R) = \int \frac{9 (\sin (qR) - qRcos {(qR))}^{2}}{{(qR)}^{6}} D (R) dR \end{matrix}$ (16)

式中, q是散射矢量, R为球的半径, D( R)为高斯函数。

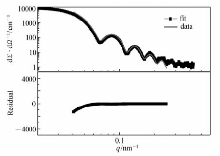
拟合曲线和相应的残差见图3。拟合尺寸为 R₀=66.9 nm, σ=2.7 nm。在获得粒子尺寸分布的情况下,可以通过粒子的比表面积或者体积分数来计算粒子的数量密度:

(17)

(18)

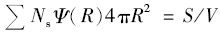
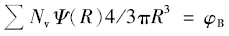
式中, S/V为粒子的比表面积, φ_B为粒子的体积分数, Ψ( R)为粒子的尺寸分布。 N_s和 N_V为两种不同算法下得到的粒子的数量密度。结果为:

N_s=4.74×10^-9 nm^-3

N_v=5.04×10^-9 nm^-3

二者的不同可能是由粒子尺寸并不完全符合高斯分布造成的。这样的数量密度相当于边长为595.2 nm 的立方体内有一个PMMA粒子。

	Figure Option View Download New Window Download As Powerpoint Slide
	图3 固含量为8.20%的PMMA乳液中粒子的尺寸拟合以及相应的残差Fig.3 The fit of size distribution of PMMA colloidal dispersion with solid content of 8.20% and the corresponding residuals

3.2 高密度聚乙烯

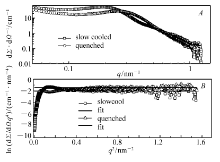
高密度聚乙烯是半结晶聚合物。从熔体冷却过程中,聚乙烯形成典型的晶区-非晶区两相体系。我们在不同热处理条件下制备了淬火和缓慢结晶的两种样品,并用DSC测试了其结晶度,分别为54.1%和60.0%。聚乙烯晶区和非晶区的密度分别为1.00和0.85 g/cm³,相应的电子密度分别为344.1和292.5 nm^-3。曝光时间为1 h。样品到探测器的距离为2400 mm。图4 A为淬火和缓慢结晶两种样品的绝对散射强度曲线。缓慢结晶样品形成的片晶厚度较大,由倒易定律,散射峰对应的q值较小。淬火样品形成的片晶厚度较小,散射曲线的峰值较大。图4 B展示了其Porod曲线。可以看到Porod曲线的尾部保持在一个常量不变,符合Porod规律。这表明高密度聚乙烯的晶区和非晶区有明显界限。对淬火和缓慢结晶样品的Porod曲线分别线性拟合(见图4 B),所得直线截距为-1.45和-1.99。求得相应的Porod常数 k_P分别为0.23和0.14 cm^-1·nm^-4。通过式(8)计算积分不变量 Q₁分别为0.97和0.79 cm^-1·nm^-3。进一步通过 Q₁可求得淬火样品的两相体积分数分别为62.9%和38.1%,缓慢结晶样品的两相体积分数分别为74.5%和25.5%。由式(7)算得相应比表面积 S/V分别为1.01×10⁹和3.22×10⁸ cm^-1。虽然淬火样品的结晶度和晶区的体积分数较小,但是其比表面积比缓慢结晶样品要高很多。

	Figure Option View Download New Window Download As Powerpoint Slide
	图4 淬火和缓慢降温的HDPE样品的绝对散射曲线( A)及相应的Porod曲线( B)Fig.4 The absolute scattering curves of quenched and slow cooled HDPE samples( A) and the corresponding Porod curves( B)

4 结论

本文通过Pilatus探测器直接测量入射光束的强度,对Xuess系统的小角X射线散射仪进行了绝对强度的校正。由于水的散射与角度无关,只取决于物理性质等温压缩率,通过水的绝对强度的校正验证了上述方法可行。通过建立的校正方法给出了两个高分子体系的应用实例:PMMA乳液和高密度聚乙烯。对这两种聚合物体系进行绝对强度的校正,计算得到相应散射体的体积分数和比表面积。 PMMA的体积分数与通过密度算得的结果很接近。淬火的高密度聚乙烯的比表面积比缓慢降温的大。

参考文献

View Option

[1]	Kratky O, Porod G, Kahovec L. Einige Neuerungen in der Technik und Auswertung von Röntgen-Kleinwinkelmessungen[J]. Z Elektrochem, 1951, 55(1): 53-59. [本文引用:2]
[2]	Orthaber D, Bergmann A, Glatter O. SAXS Experiments on Absolute Scale with Kratky Systems Using Water as a Secondary Standard[J]. J Appl Crystallogr, 2000, 33(2): 218-225. [本文引用:2]
[3]	Lin J S, Hendricks R W, Schultz J M, et al. Absolute Integrated SAXS Measurements During the Crystallization of Linear Polyethylene[J]. J Polym Sci: Polym Phy Ed, 1982, 20(8): 1365-1369. [本文引用:1]
[4]	Luzzati V. Interprétation des Mesures Absolutes de Diffusion Centrale des Rayons-X en Collimation Ponctuelle ou Linéaire - Solutions de Particules Globulaires et de Batonnets[J]. Acta Cryst, 1960, 13(11): 939-945. [本文引用:1]
[5]	Weinberg D L. Absolute Intensity Measurements in Small-angle X-ray Scattering[J]. Rev Sci Instrum, 1963, 34(6): 691-696. [本文引用:1]
[6]	Damaschu. G, Muller J. Die Messung der Absolutintensität der Röntgen-Kleinwinkelstreuung Durch Schwächung des Primärstrahls mit Absorptionsfiltern Nach Vorheriger Monochroma Tisierung Durch Totalreflexion[J]. Z Naturforsch A-Astrophys Phys Phys Chem, 1965, A20(10): 1274-1279. [本文引用:1]
[7]	Kratky O, Wawra H. Messungen der Abxolutintensität der Diffusen Röntgenkleinwinkelstreuung Durch Mechanische Schwächung des Primärstrahls bei Anwendung der Impulszähltechnik[J]. Monatsh Chem, 1963, 94(5): 981-987. [本文引用:1]
[8]	Stabinger H, Kratky O. A New Technique for the Measurement of the Absolute Intensity of X-ray Small Angle Scattering. The Moving Slit Method[J]. Makromol Chem, 1978, 179(6): 1655-1659. [本文引用:1]
[9]	Dreiss C A, Jack K S, Parker A P. On the Absolute Calibration of Bench-top Small-angle X-ray Scattering Instruments: A Comparison of Different Standard Methods[J]. J Appl Crystallogr, 2006, 39(1): 32-38. [本文引用:3]
[10]	Kratky O, Pilz I, Schmitz P J. Absolute Intensity Measurement of Small Angle X-ray Scattering by Means of a Standard Sample[J]. J Colloid Interface Sci, 1966, 21(1): 24-34. [本文引用:1]
[11]	Pilz I, Kratky O. Absolute Intensity Measurement of Small-angle X-ray Scattering by Means of a Standard Sample, Ⅱ[J]. J Colloid Interface Sci, 1967, 24(2): 211-218. [本文引用:1]
[12]	Pilz I. Absolute Intensity Measurement of Small-angle X-ray Scattering by Means of a Standard Sample, Ⅲ[J]. J Colloid Interface Sci, 1969, 30(1): 140-144. [本文引用:1]
[13]	Shaffer L B, Hendrick R W. Calibration of Polyethylene(Lupolen) as a Wavelength-Independent Absolute Intensity Standard[J]. J Appl Crystallogr, 1974, 7(2): 159-162. [本文引用:1]
[14]	Endres A, Lode U, Vonkrosigk G, et al. X-ray Absolute Intensity Measurement at HASYLAB Ultrasmall Angle X-ray Scattering Beamline BW4[J]. Rev Sci Instrum, 1997, 68(11): 4009-4013. [本文引用:2]
[15]	Russell T P. An Absolute Intensity Standard for Small-angle X-ray Scattering Measured with Position-sensitive Detectors[J]. J Appl Crystallogr, 1983, 16(5): 473-478. [本文引用:1]
[16]	Russell T P, Lin J S, Spooner S, et al. Intercalibration of Small-angle X-ray and Neutron-Scattering Data[J]. J Appl Crystallogr, 1988, 21(6): 629-638. [本文引用:3]
[17]	Hermans P H, Heikens D, Weidinger A. A Quantitative Investigation on The X-ray Small Angle Scattering of Cellulose Fibers. 2. The Scattering Power of Various Cellulose Fibers[J]. J Polym Sci, 1959, 35(128): 145-165. [本文引用:1]
[18]	Zheng N, Yi Z Y, Li Z Z, et al. Achieving Grazing-Incidence Ultra-small-angle X-ray Scattering in A Laboratory Setup[J]. J Appl Crystallogr, 2015, 48(2): 608-612. [本文引用:1]
[19]	MO Zhishen, ZHANG Hongfang, ZHANG Jidong. Structure of Crystalline Polymers by X-Ray Diffraction[M]. 2nd Ed. Beijing: Science Press, 2010: 346-349(in Chinese). 莫志深, 张宏放, 张吉东. 晶态聚合物结构和X射线衍射[M]. 第2版. 北京: 科学出版社, 2010: 346-349. [本文引用:1]

1951

0.0

... 绝对强度用来计算与质量密度有关的参数,如相对分子质量^[1-2]和电子密度差^[3]等 ...

... 第2种称为间接法,即标样法,是用已知绝对强度的样品,如水^[2,9]、聚乙烯^[10-14]、二氧化硅悬浮液^[9,15-16]、玻璃碳^[9,16]和金溶胶^[1,17]等,作为标准样品,用与研究样品相同的测试条件测试标准样品的散射强度,将研究试样的相对散射强度转化成绝对散射强度 ...

2000

0.0

... 绝对强度用来计算与质量密度有关的参数,如相对分子质量^[1-2]和电子密度差^[3]等 ...

1982

0.0

... 绝对强度用来计算与质量密度有关的参数,如相对分子质量^[1-2]和电子密度差^[3]等 ...

1960

0.0

... 目前绝对强度的校正方法有两种:第1种称为衰减法或直接法,是用不同厚度的吸收箔^[4-6](如Ni片等)或者特殊机械装置(如旋转圆片^[7]和移动狭缝^[8]等)来衰减入射光强,使之达到可准确测量的范围,然后外推出入射光强 ...

1963

0.0

1965

0.0

1963

0.0

1978

0.0

2006

0.0

1966

0.0

1967

0.0

1969

0.0

1974

0.0

1997

0.0

... 其中立体角的定义^[14]是: ...

1983

0.0

1988

0.0

... 1 原理微分散射截面的定义^[16]是单位时间单位立体角被散射的光强与入射光强(counts/(cm²#cod#x000b7 ...

1959

0.0

2015

0.0

... 样品到探测器的距离也是可调节的,能实现从小角到超小角的测试^[18] ...

2010

0.0

... 由图2B可知,Porod曲线有正偏离现象,原因是水的热密度起伏造成的^[19] ...