Loading [MathJax]/jax/output/HTML-CSS/jax.js
引用本文
张锦, 周诗岽, 卢国维, 严红玉, 赵永利. 水合物反应液中水活度系数模型研究进展[J]. 应用化学, 33(3): 277-283
ZHANG Jin, ZHOU Shidong, LU Guowei, et al. Research Development of Activity Coefficient Models in Hydrate Reaction Media[J]. Chinese Journal of Applied Chemistry, 33(3): 277-283  
Permissions
Copyright©2016, 应用化学编辑部
本文属于开放获取期刊，遵循CCAL协议，使用请注明出处。
水合物反应液中水活度系数模型研究进展
张锦, 周诗岽*, 卢国维, 严红玉, 赵永利
常州大学油气储运技术省重点实验室 江苏 常州 213016
通讯联系人:周诗岽,副教授; Tel/Fax:0519-83290280; E-mail:zsd@cczu.edu.cn; 研究方向:天然气水化物技术
收稿日期:2015-06-24 修回日期:2015-08-13 接受日期:2015-09-25
基金:国家自然科学基金(51176015),常州市工业支撑项目(CE20140055),常州大学大学生科技创新基金项目(201504A17);
摘要

水合物反应液中水活度系数的计算对水合物相平衡特性的研究及水合物技术的应用具有重要意义。 通过调研大量的国内外资料,概括了Margules、Wilson、NRTL、UNIQUAC及UNIFAC活度系数方程及其关联式等模型及其应用,结果表明,Margules模型常用于二元体系活度系数的计算,但对高温高压体系条件下的溶液适用性较差;Wilson模型参数回归误差稍大且不适于溶质与离子不能完全互溶体系;UNIQUAC模型在含水或咪唑类离子反应液体系中误差较大;多元离子体系相平衡的研究中常选择NRTL模型;UNIFAC模型拟合效果较好,可实现较高浓度体系活度系数的精确计算,应用较广泛。 水活度关联方程参数拟合效果好,且准确度高,但在高温高压水合物反应液体系中的计算仍是一个技术难点,是今后的研究方向。

关键词: 水合物; 活度系数模型; 添加剂; 相平衡
中图分类号:O642.4 文献标志码:A 文章编号:1000-0518(2016)03-0277-07
Research Development of Activity Coefficient Models in Hydrate Reaction Media
ZHANG Jin, ZHOU Shidong, LU Guowei, YAN Hongyu, ZHAO Yongli
Jiangsu Key Laboratory of Oil and Gas Storage and Transportation Technology, Changzhou University,Changzhou,Jiangsu 213016,China
Corresponding author:ZHOU Shidong, associate professor; Tel/Fax:0519-83290280; E-mail:zsd@cczu.edu.cn; Research interests:natural gas hydrate technology
Received:2015-06-24 Revised:2015-08-13 Accepted:2015-09-25
Fund:Supported by the National Natural Science Foundation of China(51176015),Changzhou Industrial Support Project(CE20140055),Changzhou University College of Science and Technology Innovation Fund Projects (No201504A17)
Abstract

Activity coefficient calculation is of great significance to the phase equilibrium of hydrate and the development of hydrate technology. Margules, Wilson, NRTL, UNIQUAC and UNIFAC models were studied by large amounts of survey with detailed analysis. The results show that Margules activity coefficient model is widely used in binary systems. Wilson activity coefficient model is not suitable for the system that solute and ion can not mix completely. The error of UNIQUAC in the calculation of aqueous or imidazole ion is bigger. We often choose NRTL for multiple ion systems. UNIFAC is widely used and can achieve precise calculation in high concentration solutions. Activity correlation equation parameters can be fit very well with high accuracy, but it is still difficult for systems of high temperature and pressure and needs to be developed in the future.

Keyword: hydrate; activity coefficient model; additive; equilibrium

气体水合物是由气体分子和水分子在低温、高压条件下相互作用而形成的一种非化学计量的笼型络合物[1]。 目前,基于水合物的生成特性及其理化性质,开发出了水合物气体分离技术[2]、水合物蓄冷技术[3]、水合物海水淡化技术[4]等一系列水合物法应用技术。 水合物应用技术的研究主要集中在水合物的快速生成,而当前的研究表明化学强化是水合物高效快速生成最具潜力的手段,对水合物技术的工业化应用实践具有重要的意义。 此外,管输天然气水合物的动态防治技术的相关研究表明,引入相关的添加剂能够极大的提高气体水合物的生成条件,抑制水合物的生成。 然而,相关的促进剂和抑制剂的性能评价必须以其对气体水合物生成特性的影响为基础,而反应液中气体水合物生成的热力学行为是水合物在生成过程中所呈现的一切宏观特性的直接原因,因此相关的热力学研究显得至关重要。 当前气体水合物生成热力学研究表明,添加剂等新组分的引入会使得水合物反应液的有效浓度与实际浓度相偏离,从而改变水溶液的活度,进而影响热力学行为。 基于此,文章调研了大量的国内外资料,对比分析了不同水活度系数计算方程的适用范围及拟合效果。

1 活度系数的影响因素及其作用机理
1.1 活度系数的影响因素

活度系数是表征水合物性质的一个重要指标[5],对活度系数大小的测定,在气体水合物形成及分解过程的研究中具有重要意义。 水合物反应液中水的活度系数的大小主要受体系温度、水的介电常数及离子的浓度等影响。

1.2 活度系数对水合物反应液的作用

在水合物反应液中,活度系数反映了有效浓度偏离实际浓度的程度[6],其数值的大小表征了溶液中水分子的无序性,水分子的活度越小,其活跃性越高,溶液中有序的水分子越少,则形成笼型络合物结构的水分子越少,因此越不利于气体水合物晶体结构的形成,这就是活度系数影响水合物形成条件的作用机理。 在纯水介质体系中,水分子间可以相互自由结合形成氢键,而当体系中有盐类物质时,削弱了水分子间的强相互作用,为使体系能量最低,盐类粒子将向最大程度形成氢键的方向定位,进而形成水合物笼型晶体结构。 而醇类物质与水分子间主要是非荷电基团对水分子产生的强相互作用,该作用力会破坏水分子通过氢键结合而成的网格结构,此时形成笼型络合物结构就需要额外的能量来克服该作用力,从而改变水合物形成的相平衡条件[7]。

2 活度系数方程

溶液中存在水合物生成促进剂或抑制剂时,活度系数大小可由状态方程或活度系数方程计算得出。 当前,常用于预测气体水合物相平衡条件的活度系数模型主要有①无规溶液活度系数方程、②局部组成活度系数方程:Wilson方程、非随机双液NRTL方程及通用似化学UNIQUAC模型和③基团贡献法UNIFAC模型及其关联式等。

2.1 无规溶液活度系数模型

Margules方程在正规溶液基础上发展而来的无规溶液模型,它是将二组分均相体系的活度系数与溶液组成相关联的经验方程,旨在解决二元体系活度的计算问题。

ln(αw,al/xw)=(1-xw)2{A+2(A-B)xw}(1)

式中, A、 B定义为:

A=a1+a2·10-3T;B=b1+b2·10-3T

式中, xw表示在含盐类和可溶性气体溶液中水的摩尔分数; T表示体系温度; a、 b分别表示温度的修正系数; α表示溶液的有效浓度。

王宜辰等[8]采用简化形式的Margules方程论述二元溶液组分分压对Raoult定律的偏差类型存在的弊端作了分析,并应用二常数的Margules方程讨论了组分分压对理想行为的偏差性质,发现只有当该方程指数项中含有足够多的项时,对实验所观测到的分压才能十分准确的加以表达。 此外,他还指出了在该方程中至少应含有二个常数的必要性。

吴大可等[9]分别采用Margules方程和Wilson方程对250~280 K温度范围内的二氧化碳与正丁烷及二氧化碳与异丁烷二元体系活度系数进行了多达140次的计算,并对比计算结果的精确度,结果发现前者以数量级之差优于后者。

Torres等[10]采用Margules方程对二元离子交换系统进行了相关计算,结果发现等温条件下,能实现高浓度体系活度系数的精确计算。

Margules方程常用于醇类介质体系水合物生成过程中水活度系数的计算。 攻克了Pitzer方程仅适用于浓度低于6 mol/kg的难点,能应用于常温下较高浓度活度系数的计算,但在高温、高压下的活度系数的计算中不是很理想,且其存在参数较少会导致二元溶液组分偏差较大的缺陷,限制了其发展。

2.2 基于局部组成的活度系数模型

局部组成概念认为溶液中分子呈不均匀分布状态,基于该理论而建立的活度系数计算模型主要有Wilson方程、NRTL方程和UNIQUAC方程。

①Wilson方程

Wilson方程基于局部组成概念,是在二组分体系数据的基础上,与Flory-Huggins溶液理论GE相结合,计算多组分非理想体系的水活度系数。 Wilson模型的表达式为:

(2)

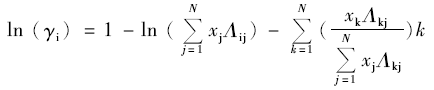式中, Λij、 Λkj分别表示的体系的特征参数; xj表示溶液中组分j的摩尔分数; xk表示溶液中组分k的摩尔分数。

金彰礼等[11]曾采用Wilson方程对汽相组分的活度系数进行了计算,选取在汽相存有缔合现象的羧酸水溶液进行关联,并初次实现了用活度系数方程关联汽液平衡,结果优于Shah的计算。

王皓等[12]将Wilson活度系数模型应用于离子液相平衡研究中,并进行了参数回归,拟合效果发现,该模型难以准确地描述具有混溶间隙特征的离子液体体系,参数拟合效果较差。

Sivamohan等[13]基于固体颗粒的溶解度和分子间的相互作用势,将基团与Wilson活度系数模型关联,导出一种包含温度、压力和浓度3个参数的新型Wilson活度系数半经验方程式。 他们将其应用于含酸、铵、碳氢化合物等75组可溶性固体颗粒溶液体系活度系数计算中,并将计算结果与实验值对比,发现绝对平均偏差约为9%,精确度良好。

Wilson方程是基于局部组成概念最先提出的活度系数计算模型,常用于二组分体系中水活度系数的计算,这为二元参数推算多元混合物的活度系数提供了可能,虽然准确度高,但其在溶质与离子互溶体系中的应用具有一定的局限性。

②NRTL方程

针对Wilson模型的局限性,Renon、Prausnitz等在双流体理论的基础上对局部组成关系式进行修正,提出了NRTL方程,其参数从相平衡数据中拟合得到,而对于非无规参数 α的取值,大多数溶液取0.3。 之后,Chen将Pitzer-Debye-Hückel理论与局部组成模型与NRTL方程结合,用于电解质溶液活度系数的计算中。

(3)

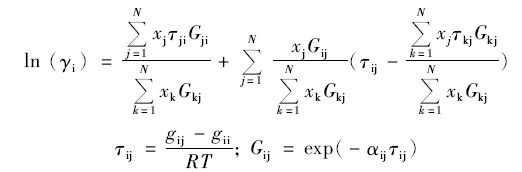式中, gij- gii是能量参数, αij成为非无规参数,且 αij= αji= α, xj表示溶液中组分j的摩尔分数; xk表示溶液中组分k的摩尔分数; τij、 Gij为模型参数。

Vatani等[14]基于遗传算法(Genetic Algorithm),采用NRTL和Two-Suffix Margules模型分别计算了20种随机抽取的三元离子液体系水活度系数,并比较了其方差。 发现分别使用NRTL和Two-Suffix Margules模型计算,其方差在0.0039~0.0195变化,在液-液平衡体系中,NRTL比Two-Suffix Margules拟合效果更好,数据更精确。 此外,基于遗传算法的NRTL模型,其方差仅为0.0039~0.0159,数据波动性小,拟合效果更稳定,且这种方法也适用于其它体系相平衡的研究中。

NRTL方程基于Wilson活度系数模型,将能量参数、非无规参数等因素考虑在内,并引入双流体理论加以修正,涉及的参数从相平衡数据中拟合均可得到,克服了Wilson模型的缺陷,能实现液相不完全互溶体系活度系数的计算。

③UNIQUAC方程

UNIQUAC模型是将NRTL方程与似化学方法相结合得出,其表达式如下:

lnγ1=lnγC1+lnγR1lnγC1=lnϕ1x1+Z2q1lnθ1ϕ1+ϕ2(l1-r1r2)l2lnγR1=q1ln(θ1+θ2τ21)+θ2q1(τ21θ1+θ2τ21-τ21θ1τ21+θ2)(4)

式中, Z表示水合物相摩尔分数(常取10); θ表示面积比; q表示结构面参数; ϕ1表示局部逸度系数; l表示析水量; x1表示液相的摩尔分数; r表示气体的结构体积参数; τ21为模型参数。 公式将面积比 θ、水合物相摩尔分数 Z(常取10)、气体的结构体积参数 r、结构面参数 q等因素考虑在内,提高了活度系数计算的精确度。

Nasrifar等[15,16,17]研究了电解质溶液、醇溶液及含CO2等可溶性气体的反应液中水合物的生成条件,只要分别计算出在3种体系中水的活度便可得出溶液活度系数,而无需依赖相互作用参数或曲线拟合参数等繁杂步骤。

Moshfeghian、Maddox、Javanmardi和Moshfeghian等将上式与经典的范德华模型结合进行修正,并得到新的相平衡温度方程,且方程认为盐类离子与醇类间无相互作用力。

lnαw=-ΔHnR(1T-1T0)(5)

式中, αw为水的活度,Δ H为水合物形成体系焓变, n为水合数, R为通用气体常数, T0为纯水溶液的初始温度。

Kang等[18]提出了评价UNIQUAC活度系数方程的新方法,将其写成Flory-Huggins和Starvermann-Guggenheim参数的关联式,并对UNIQUAC参数进行拟合,发现数据拟合精确度提高,且计算量减少。

Hajar等[19]将GE-EOS与UNIQUAC活度系数模型结合以预测纯水及含可溶性气体体系中水合物形成的温、压条件。 其中,UNIQUAC直接从水合物生成实验数据中取得二元参数,旨在测定气-液-水合物三元体系中水的活度系数,避免了必须依赖气、液相平衡数据的难题。 此外,GE-EOS与UNIQUAC方程的结合,简化了计算步骤。

Haghtalab等[20]基于吉布斯自由能理论,导出了二元非电解质体系水活度系数UNIQUAC-NRF计算模型,该模型与实验值拟合效果较好。 随后,他们又采用UNIFAC-NRF[21,22]活度系数模型研究了CH4、C2H6、CO2和N2体系中气液相平衡条件,发现UNIFAC-NRF参数拟合效果均比LCVM-UNIFAC、GE-EOS等模型精确度高。 在此基础上,他们又采用活度系数模型预测了CO2、H2S等酸性气体在不同体系中的溶解度,发现在MDEA(Methyldiethanolamine)-CO2-H2O体系中,Clegg-Pitzer与N-Wilson-NRF模型相比,前者的拟合效果更精确,但对于二者的优选问题仍存在争议。 而对于MEA(Monoethanolamine)-CO2-H2O体系,N-Wilson-NRF比Clegg-Pitzer模型的数据拟合更精确。 此外,在MEA和AMP(2-Amino-2-Methyl-1-Propanol)体系中,N-Wilson-NRF与UNIQUAC-NRF模型相比,前者计算步骤简洁直观,更具优势。

王皓等[12]将Wilson、NRTL和UNIQUAC 3种活度系数模型应用于离子液体相平衡研究中,并进行了参数回归,拟合效果分析发现,Wilson模型在溶质与离子不能完全互溶体系中,参数拟合效果较差。 此外,UNIQUAC模型参数回归效果良好,但对于含水或咪唑类离子液体体系,误差仍较大。 且二者对体系组成的依赖性强,参数回归效果不稳定,对三元体系的预测能力也有一定局限性。 而NRTL活度系数模型在三元体系中的回归或预测中效果均较好,尤其在离子液体摩尔分数在0.055~0.12时,优势更明显。 因此,在多元离子体系相平衡的研究中常选择NRTL活度系数模型。

2.3 基团贡献法

UNIFAC模型是将化合物按基团划分,将物质的物性看作由组成该物质的分子中各基团对物性贡献的加和。 此时,用有限的基团特性参数关联多种物质的性质,近似假设某一基团在分子中的作用与其它基团无关,进而推算未知体系的物性。 其表达式为:

lnζSRi=lnζUNIFACi=lnζCi+lnζRi(6)

式中, ζCi表示组合项的熵对活度系数的贡献度, ζRi表示剩余项的焓对活度系数的贡献度。

Erdakos等[23]采用X-UNIFAC法预测了溶解有机化合物及无机盐的液相溶胶颗粒体系中水的活度系数,并分别用于电解质溶液(离子浓度不大于30 mol/kg)和有机化合物+无机盐水溶液(离子浓度不大于10 mol/kg)体系中水活度系数的计算。 结果表明,计算值与实验结果平均偏差仅为4%,拟合效果较好。

Mohammadi等[24]提出水合物反应液中甲醇、乙醇、NaCl、KCl等水合物生成抑制剂的存在强烈作用于水活度系数,从而改变水合物分解的温、压条件。 此外,他们认为低浓度条件下,抑制剂的种类并不影响水活度系数大小。 此时,热力学模型可以准确的预测活度系数,并为抑制剂体系中准确预测水合物分解相平衡提供保障。

Moradia等[25]基于van der Waals-Platteeuw方程,采用UNIQUAC-NRF活度系数计算模型,预测了盐溶液、醇溶液及其混合物等热力学抑制剂体系中水合物的形成条件。 对比UNIFAC、UNIQUAC和UNIQUAC-NRF 3种模型,发现UNIQUAC-NRF模型与实验数据拟合效果较好,而UNIFAC与UNIQUAC仅在甲烷、乙烷体系中效果较好。 此外,E-UNIQUAC-NRF与UNIQUAC均适用于电解质溶液、醇溶液及其混合物反应液中水活度系数的计算,且前者在CH4-N2-NaCl体系中,最大偏差达6.36%,精确度更高。

Paduszynski等[26]将修订后的UNIFAC方程用于哌啶离子液体系中水活度系数的计算。 实验结果表明,计算值与实验值的平均偏差几乎为零,参数拟合精确度较高。

UNIFAC方程常用于电解质溶液体系活度系数的计算,具有利用少量基团预测多种化合物体系相平衡的特性,能实现较高浓度体系水活度系数的计算,极具灵活性和应用性,是目前应用最广泛的活度系数模型。

综合以上分析,几种活度系数模型均可用于二元体系,而对于多元体系,NRTL参数拟合精确度较Wilson、UNIQUAC两种模型高。 Wilson模型常用于二组分体系中水活度系数的计算,在溶质与离子不能完全互溶体系有一定的局限性。 UNIQUAC计算步骤精简,且参数回归效果良好,但对于含水或咪唑类离子液体的体系,误差较大。 NRTL与UNIFAC方程均适用于电解质溶液活度系数的计算,Margules模型与UNIFAC方程均可实现较高浓度溶液活度系数的精确计算,但前者在高压体系中水活度系数的计算中误差较大。 此外,相关联的活度系数模型较单一活度系数计算模型的参数拟合效果好,精确度更高。

3 结 语

天然气水合物反应液中水活度系数的计算对水合物相平衡特性研究及水合物技术的应用至关重要。文章综合对比分析了不同水活度系数方程及其关联式等模型的应用,并得出以下结论:

1)无规溶液Margules活度系数模型常用于二元体系活度系数的计算,能实现常温下较高浓度体系中水活度系数的计算,但对高温高压体系条件下的溶液适用性较差;

2)基于局部组成的活度系数方程中,Wilson模型回归参数误差稍大,且其在溶质与离子不能完全互溶体系中的应用具有一定的限制性;UNIQUAC模型参数回归效果良好,但对于含水或咪唑类离子液体的体系误差仍较大;NRTL模型在三元离子液体系中的参数拟合效果较好,因此,在多元离子液体系相平衡的研究中,常采用NRTL活度系数模型;

3)UNIFAC模型灵活性较强,模拟效果较好,可实现较高浓度体系水活度的计算,应用较广泛。 对于UNIFAC-NRF及UNIQUAC-NRF等关联的水活度模型,参数拟合效果较好,准确度更高,但对于高温、高压水合物反应液体系中的计算仍是一个技术难点,是今后的研究方向。

参考文献
[1] Eslamimanesh A, Mohammadi A H, Richon D, et al. Application of Gas Hydrate Formation in Separation Processes: A Review of Experimental Studies[J]. J Chem Thermodyn, 2012, 46(3): 62-71. [本文引用:1]
[2] Artem A S, Andrey Y M, Tatyana V R. Methane Capacity of Double Tetrabutylammonium Bromide+Methane Ionic Clathrate Hydrates[J]. Energy Fuels, 2012, 26(6): 3711-3716. [本文引用:1]
[3] Karimi R, Varaminian F, Izadpanah A A, et al. Effects of Different Surfactants on Ethane Hydrate Formation Kinetics: Experimental and Modeling Studies[J]. Energy Technol, 2013, 1(9): 530-536. [本文引用:1]
[4] Zhou S D, Yu Y S, Zhao M M, et al. Effect of Graphite Nanoparticles on Promoting CO2 Hydrate Formation[J]. Energy Fuels, 2014, 28(7): 4694-4698. [本文引用:1]
[5] WU Qiang, ZHAO Meirong, GAO Xia. Effect of Propane on Phase Equilibrium of Gas Hydrate[J]. J Heilongjiang Univ Sci Technol, 2014, 24(1): 38-42(in Chinese).
吴强, 赵美蓉, 高霞. 丙烷对瓦斯水合物相平衡条件的影响[J]. 黑龙江科技大学学报, 2014, 24(1): 38-42. [本文引用:1]
[6] LIU Changling, YE Yuguang, SUN Shicai, et al. The P-T Gas Hydrate Stability under Different Systemconditions and Influencin Factors of Experimental Research[J]. China Sci: Earth Sci, 2013, 43(3): 406-413(in Chinese).
刘昌岭, 业渝光, 孙始财, 等. 不同体系下天然气水合物P-T稳定条件及其影响因素的实验研究[J]. 中国科学: 地球科学, 2013, 43(3): 406-413. [本文引用:1]
[7] XU Xianzhen. Electrolyte Solution Activity Coefficient Model[D]. Ocean University China, 2013(in Chinese).
徐显朕. 电解质溶液活度系数模型的研究[D]. 中国海洋大学, 2013. [本文引用:1]
[8] WANG Yichen. A Problem in the Applications of Margules Equation[J]. J Yantai Teachers Univ(Nat Sci Edit), 1992, 8(1/2): 112-114(in Chinese).
王宜辰. Margules方程应用中的一个问题[J]. 烟台师范学院学报(自然科学版), 1992, 8(1/2): 112-114. [本文引用:1]
[9] WU Dake, CHEN Shulin. Carbon Dioxide/n-Butane, CO2/isobutane Binary System Activity Coefficient Is Calculated[J]. J Guizhou Inst Technol, 1996, 25(2): 30-33(in Chinese).
吴大可, 陈树琳. 二氧化碳/正丁烷、二氧化碳/异丁烷二元系活度系数计算[J]. 贵州工学院学报, 1996, 25(2): 30-33. [本文引用:1]
[10] Torres J C, Jose C G. Prediction of Ion-interaction Parameters of Binary 2: 1 and 2: 2 Ion-exchange Systems by the Coupling of the Margules Model with a Linear Free Energy Correlation Approach[J]. Micropor Mesopor Mater, 2009, 126(1/2): 182-191. [本文引用:1]
[11] JIN Zhangli, QIU Daofa. Vapor Vhase Component Activity Coefficient was Calculated by the Wilson Equation[J]. Chem Eng, 1988, 1(1): 27-32(in Chinese).
金彰礼, 邱道发. 用Wilson方程计算汽相组分活度系数[J]. 化学工程, 1988, 1(1): 27-32. [本文引用:1]
[12] WANG Hao, LU Kang, PENG Xuan. Based on Wilson, UNIQUAC and NRTL Activity Coefficient Model System of Ionic Liquid Phase Equilibrium[J]. J Beijing Univ Chem Ind(Nat Sci Edn), 2013, 40(1): 10-15(in Chinese).
王皓, 陆康, 彭璇. 基于Wilson、UNIQUAC和NRTL活度系数模型的离子液体体系的相平衡比较[J]. 北京化工大学学报(自然科学版), 2013, 40(1): 10-15. [本文引用:2]
[13] Sivamohan N R, Giridhar M. An Association and Wilson Activity Coefficient Model for Solubilities of Aromatic Solid Pollutants in Supercritical Carbon Dioxide[J]. Therm Acta, 2012, 541(10): 49-56. [本文引用:1]
[14] Mostafa V, Morteza A, Gholamreza V N. Application of Genetic Algorithm to the Calculation of Parameters for NRTL and Two-Suffix Margules Models in Ternary Extraction Ionic Liquid Systems[J]. J Ind Eng Chem, 2012, 18(5): 1715-1720. [本文引用:1]
[15] Nasrifar K, Ayatollahi S, Moshfeghian M. Generalized Saturated Liquid Density Prediction Method for Pure Compounds and Multi-component Mixtures[J]. Fluid Phase Equilib, 2000, 168(1): 71-90. [本文引用:1]
[16] Nasrifar K, Moshfeghian M. A New Cubic Equation of State for Simple Fluids: Pure and Mixture[J]. Fluid Phase Equilib, 2001, 190(1/2): 73-88. [本文引用:1]
[17] Nasrifar K, Moshfeghian M. Vapor Liquid Equilibria of LNG and Gas Condensate Mixtures by the Nasrifar Moshfeghian Equation of State[J]. Fluid Phase Equilib, 2002, 200(1): 203-216. [本文引用:1]
[18] Kang J W, Vladimir D, Robert D C, et al. A New Method for Evaluation of UNIFAC Interaction Parameters[J]. Fluid Phase Equilib, 2011, 309(1): 68-75. [本文引用:1]
[19] Hajar D, Haghtalab A. Prediction of Hydrate Formation Conditions Using GE-EOS and UNIQUAC Models for Pure and Mixed-gas Systems[J]. Fluid Phase Equilib, 2014, 369(15): 1-12. [本文引用:1]
[20] Haghtalab A, Mohammad A A. An Excess Gibbs Energy Model to Study the Phase Behavior of Aqueous Two-phase Systems of Polyethylene Glycolqdextran[J]. Fluid Phase Equilib, 2000, 171(1/2): 77-90. [本文引用:1]
[21] Haghtalab A, Peyman M. Vapor-liquid Equilibria of Asymmetrical Systems Using UNIFAC-NRF Group Contribution Activity Coefficient Model[J]. Fluid Phase Equilib, 2010, 289(1): 61-71. [本文引用:1]
[22] Haghtalab A, Abolfazl S. Modeling Solubility of Acid Gases in Alkanolamines Using the Nonelectrolyte Wilson-nonrandom Factor Model[J]. Fluid Phase Equilib, 2010, 289(1): 6-14. [本文引用:1]
[23] Garnet B E, Elsa I C, James F P, et al. Prediction of Activity Coefficients in Liquid Aerosol Particles Containing Organic Compounds, Dissolved Inorganic Salts and Water-Part 3: Organic Compounds, Water and Ionic Constituents by Consideration of Short-, mid-, and Long-range Effects Using X-UNIFAC. 3[J]. Atmos Environ, 2006, 33(40): 6437-6452. [本文引用:1]
[24] Mohammadi A H, Dominique R. Phase Equilibria of Clathrate Hydrates of Methyl Cyclopentane, Methyl Cyclohexane, Cyclopentane or Cyclohexane+carbon dioxide[J]. Chem Eng Sci, 2009, 24(64): 5319-5322. [本文引用:1]
[25] Moradia S, Haghtalabb A, Alireza F. Prediction of Hydrate Formation Conditions in the Solutions Containing Electrolyte and Alcohol Inhibitors and Their Mixtures Using UNIQUAC-NRF models[J]. Fluid Phase Equilib, 2013, 15(349): 61-66. [本文引用:1]
[26] Paduszynski K, Urszula D. Extension of Modified UNIFAC(Dortmund) Matrix to Piperidinium Ionic Liquids[J]. Fluid Phase Equilib, 2013, 353(15): 115-120. [本文引用:1]