Processing math: 100%
引用本文
李晓萱, 陈涛, 伍胜利. 水性聚氨酯/功能化石墨烯纳米复合材料的非等温结晶动力学[J]. 应用化学, 32(11): 1319-1326
LI Xiaoxuan, CHEN Tao, WU Shengli. Non-isothermal Crystallization Kinetics of Waterborne Polyurethane/functionalized Graphene Nanocomposites[J]. Chinese Journal of Applied Chemistry, 32(11): 1319-1326  
Permissions
Copyright©2015, 应用化学编辑部
本文属于开放获取期刊，遵循CCAL协议，使用请注明出处。
水性聚氨酯/功能化石墨烯纳米复合材料的非等温结晶动力学
李晓萱a*, 陈涛a, 伍胜利a,b
a合肥工业大学化学工程学院 合肥 230009
b安徽省食品药品检验研究院 合肥 230051
通讯联系人:李晓萱,副教授; Tel:0551-62931450; E-mail:lxx2000@sohu.com; 研究方向:精细化工和绿色化学
收稿日期:2015-04-29 修回日期:2015-07-24 接受日期:2015-08-04
基金:安徽省高等学校自然科学研究资助项目(KJ2012B141);
摘要

采用差示扫描量热法DSC研究了水性聚氨酯/功能化石墨烯(WPU/FGNs)纳米复合材料的非等温结晶行为,分别采用Ozawa方程、莫志深方程研究复合材料的非等温结晶动力学,并通过Kissinger方程计算了结晶过程中的活化能。 结果表明,石墨烯在复合材料的结晶过程中起到异相成核剂的作用,提高了复合材料的结晶起始温度、峰值温度和结晶速率;增加石墨烯的质量分数,复合材料的结晶维数增加;石墨烯增加至0.3%,复合材料的活化能从-47.74 kJ/mol降低至-53.60 kJ/mol,继续增加石墨烯至1.0%,复合材料的活化能增加至-41.74 kJ/mol。

关键词: 石墨烯; 水性聚氨酯; 非等温结晶; 结晶动力学
中图分类号:O632.6 文献标志码:A 文章编号:1000-0518(2015)11-1319-08
Non-isothermal Crystallization Kinetics of Waterborne Polyurethane/functionalized Graphene Nanocomposites
LI Xiaoxuana, CHEN Taoa, WU Shenglia,b
aSchool of Chemical Engineering,Hefei University of Technology,Hefei 230009,China
bAnhui Institute of Food and Drug Control,Hefei 230051,China
Corresponding author:LI Xiaoxuan, associate professor; Tel:0551-62931450; E-mail:lxx2000@sohu.com; Research interests:fine chemicals and green chemistry
Received:2015-04-29 Revised:2015-07-24 Accepted:2015-08-04
Fund:Supported by University Natural Science Research Funding Program of Anhui Province(No.KJ2012B141)
Abstract

The non-isothermal crystallization behavior of waterborne polyurethane/functionalized graphene nanocomposites(WPU/FGNs) was studied by differential scanning calorimetry(DSC). The non-isothermal crystallization kinetics of WPU/FGNs was investigated by Ozawa and Mo equations, and the crystallization activation energies were calculated by Kissinger equation. The results show that FGNs can be used as heterogeneous nucleation agent to increase the onset of crystallization temperature, peak temperature and crystallization rate of WPU during non-isothermal crystallization process of WPU/FGNs. Crystallization dimension of the composites increases with the increase of the mass fraction of FGNs. When the mass fraction of FGNs increases to 0.3%, crystallization activation energy of the composite decreases from -47.74 kJ/mol to -53.60 kJ/mol. When the mass fraction of FGNs is 1.0%, the crystallization activation energy of the composite increases to -41.74 kJ/mol.

Keyword: functionalized graphene nanocomposites; waterborne polyurethane; non-isothermal crystallization; crystallization kinetics

石墨烯是一种由碳原子以 sp2杂化轨道组成,呈蜂巢晶格的单原子层二维纳米材料。 由于石墨烯具有力学性能优异[1]、透光率高[2]、电导率高[3]、热导率大[4]和比表面积大[5]等优点,在电容器、燃料电池、传感器、透明导电薄膜等领域均具有潜在的应用[6]。 其中聚合物/石墨烯复合材料是其中最具前景的应用之一。

聚氨酯是一种以多元醇为软段、多异氰酸酯和小分子扩链剂为硬段,软段和硬段交替形成的嵌段高分子聚合物。聚氨酯的原料种类繁多,可以通过分子结构的设计制备出综合性能优异的聚氨酯产品,广泛应用于涂料、纺织、皮革等行业。 但聚氨酯的一些缺陷,如抗拉强度弱、耐热性差等限制了其在某些领域的应用。 目前,以石墨烯为填料提高聚氨酯性能的方法已取得良好的效果。 相比于传统的复合材料,纳米复合材料能极大地提高聚合物基体的各项物理性能,如导电性、阻燃性和机械性能等[7]。 Luo等[8]研究发现,当石墨烯为1.5%时,所制备的石墨烯/聚氨酯复合材料的抗拉强度较纯聚氨酯提升了41.6%。 另外,复合材料的热稳定性也有了极大的提升。 Pokharel等[9]研究表明,在不降低断裂伸长率的情况下,所制备的石墨烯为2.0%的聚氨酯纳米复合材料的抗拉强度和杨氏模量分别提升了30%和50%。 他们还发现石墨烯的加入降低了聚氨酯的硬段结晶度。

基于聚氨酯的可设计性可以制备出软段或硬段具有一定结晶度的聚氨酯材料。 高聚物的结晶过程与小分子类似,主要由晶核的形成和晶粒生长两个步骤,但高分子材料一般不会完全结晶[10],这种结晶能力差别的根本原因是不同高分子具有不同的结构特征,这些结构特征中能否规整排列形成高度有序的晶格是关键。 聚氨酯中软段和硬段的原料、有序结构和比例对结晶速率、结晶度以及结晶形态均有重要影响,从而影响材料的物理性能和使用性能[11]。 对于结晶性聚合物,石墨烯的引入对其结晶行为将产生不可忽视的作用,进而影响材料的性能。 Shehzad等[12]研究表明,在高密度聚乙烯的非等温结晶过程中,石墨烯的添加降低其结晶活化能,提高了结晶起始温度,起到了成核剂的作用。 但过量的石墨烯阻碍了晶体生长,降低了整体结晶速率。 Yang等[13]通过DSC研究了聚(3-己基噻吩)(P3HT)/石墨烯纳米复合材料的非等温结晶过程,发现石墨烯提高了P3HT的结晶峰温度和结晶度,而半结晶时间变化不大。 由此可见,研究石墨烯对聚氨酯结晶行为的影响对于拓展此类材料的应用领域具有十分重要的实际意义,但目前相关研究工作尚未见报道。

非等温结晶过程是在变化的温度场下的结晶过程,接近于实际生产过程。 研究聚氨酯非等温结晶过程对聚氨酯的配方调配、工艺流程和应用领域等有着理论指导的作用。 本文利用表面活性剂聚对苯乙烯磺酸钠(PSS)表面修饰氧化石墨烯,经水合肼还原后制得水溶性还原石墨烯,将其与结晶型水性聚氨酯物理共混后制备聚氨酯/石墨烯纳米复合材料,通过差示扫描量热仪(DSC)研究了石墨烯的引入对聚氨酯结晶行为影响。

1 实验部分
1.1 试剂和仪器

水性聚氨酯树脂(WPU)(U-54,德国拜耳公司);天然鳞片石墨粉(孔径,25 μm,青岛天盛达石墨有限公司);浓硫酸(分析纯,上海振企化学试剂有限公司);NaNO3(分析纯,天津市化学试剂批发公司);KMnO4(分析纯,上海振企化学试剂有限公司);H2O2(分析纯,江苏强盛功能化学股份有限公司);浓盐酸(优级纯,国药集团化学试剂有限公司);水合肼(分析纯,天津市大茂化学试剂厂);聚对苯乙烯磺酸钠(PSS, Mw=60000,质量分数25%,上海喜润化学工业有限公司)。

P70H型Elma超声清洗仪(德国Elma公司);204F1型差示扫描量热仪(德国耐驰公司)。

1.2 样品制备

1.2.1 氧化石墨的制备 采用改进的Hummers法[14]制备氧化石墨。 取115 mL浓硫酸、2.5 g NaNO3和5.0 g天然鳞片石墨粉于1 L烧杯中,冰水浴。 待烧杯内混合物温度降至5 ℃,少量多次加入15.0 g KMnO4,保持温度小于7 ℃,反应2 h。 升温至35 ℃,恒温反应2 h。 用恒压滴液漏斗滴加230 mL去离子水。 升温至98 ℃,反应30 min。 再在快速搅拌下加入700 mL水和15 mL H2O2,充分搅拌,静置,沉淀。 除去上层清液,用5%的盐酸清洗两遍,再用去离子水清洗一遍,然后用10000 r/min离心机离心,重复水洗离心操作直至溶液接近中性。 最后倒入透析袋中透析两天,即得氧化石墨水溶液。

1.2.2 FGNs的制备 配制200 mL 1 g/L的氧化石墨水溶液于500 mL锥形瓶中,超声1.0 h使其剥离成氧化石墨烯(Graphene Oxide,GO)。再加入PSS使PSS和G质量之比为1:1,摇匀,继续超声1.0 h。 随后将锥形瓶内的溶液倒入250 mL圆底烧瓶中,再加入0.3 g水合肼,加热至回流并保持8 h。 最后,用孔径48 μm滤布过滤即得FGNs分散液。

1.2.3 WPU/FGNs复合材料的制备 将WPU和FGNs分散液混合,磁力搅拌2 h,再将混合液倒入模具中,室温下放置24 h后置于60 ℃烘箱中干燥24 h得WPU-FGNs复合材料。 当石墨烯的质量分数分别为0.1%、0.3%、0.5%、1.0%时,所得的复合材料分别记为WPU/0.1%FGNs、WPU/0.3%FGNs、WPU/0.5%FGNs和WPU/1.0%FGNs。

1.3 DSC测试

在N2气气氛下,将5~10 mg样品置于铝坩埚中,以10 K/min的升温速率升温至423 K,恒温30 min以消除热历史,然后分别以5、10、15、20 K/min的速率降温至223 K进行非等温结晶,记录结晶过程中热流速率随时间的变化。

2 结果与讨论
2.1 WPU/FGNs纳米复合材料的非等温结晶行为

图1 WPU( A, B)和WPU/1.0%FGNs复合材料( C, D)在不同降温速率下的二次升温DSC曲线( A, C)和相对结晶度随结晶时间的变化曲线( B, D)Fig.1 DSC second heating curves( A, C) and time dependence of relative crystallinity( B, D) of WPU( A, B) and WPU/1.0%FGNs( C, D) composites at different cooling rates.

U-54由异佛尔酮二异氰酸酯(IPDI)和聚己二酸丁二醇酯二醇(PBA)为原料制成的软段结晶型聚氨酯。 通过DSC测试可以得到各个样品在不同降温速率下的结晶曲线。 如图1 A和 C分别为WPU和WPU/1.0%FGNs复合材料在不同降温速率(5、10、15、20 K/min)下的非等温结晶DSC曲线。 利用式(1)可以把热焓与温度的关系曲线转换为相对结晶度 X( t)与温度的关系曲线:

X(T)=ΔHc(T)ΔHc(T∞)=∫TT0dHcdT)dT∫T∞T0dHcdT)dT(1)

式中, T0和 T∞分别是结晶起始和终止温度;d Hc是样品在无限小温度间隔d T下的结晶焓。 根据非等温结晶过程中温度和时间的关系,通过式(2)可以得到相对结晶度随时间的关系曲线:

t=T-T0Φ(2)

表1 WPU和WPU/FGNs复合材料的非等温结晶参数 Table 1 Non-isothermal crystallization parameters of WPU and WPU/FGNs composites

式中, T为 t时刻的温度, Φ是降温速率。 如图1 B和图1 D分别为WPU和WPU/1.0%FGNs复合材料非等温结晶过程中相对结晶度随结晶时间的变化曲线。 通过非等温DSC曲线及相对结晶度随结晶时间的变化曲线,可以得到一系列非等温结晶参数,列于表1。 其中, Φ是降温速率, T0和 T∞分别是结晶起始和终止温度, Tp为结晶峰温, t1/2是半结晶时间,Δ H是整个非等温结晶过程的结晶焓。

从表1可以看出,增大降温速率,结晶放热峰的峰值温度和结晶起始点均向低温移动,结晶峰变宽且半结晶时间明显缩短。 这是由于结晶过程包括晶核的形成和晶粒生长两个主要过程。 在成核过程中,熔体中的WPU分子链作有序排列而形成晶核。 在较高的降温速率下,WPU分子链在较大的过冷度下才能完成折叠成核的过程。 在成核的短时间内,聚合物快速结晶,造成结晶整体过程向低温方向移动,结晶峰变宽,半结晶时间明显缩短。 比较各结晶峰的结晶焓(Δ H)可以看出,各个结晶过程的结晶度相差不大。 值得注意的是,在降温速率为20 K/min时,WPU的结晶焓明显低于其他温度条件下的结晶焓。 这可能是由于在剧烈降温下,WPU分子链没有形成大量晶核就被低温限制了运动,因而结晶不完整,表现为结晶焓的减小。 另外,在相同的结晶速率下,WPU/FGNs的 T0、 Tp和 T∞高于WPU,半结晶时间减小。 这说明在WPU/FGNs的非等温结晶过程中,FGNs起到异相成核的作用。 对于WPU/FGNs,增加FGNs至0.3%,复合材料的 T0、 Tp和 T∞均增加,半结晶时间降低,说明复合材料结晶能力的提高;继续增加FGNs至1.0%,复合材料的 Tp和 T0逐渐降低,半结晶时间增加,说明复合材料结晶能力降低。

2.2 WPU/FGNs纳米复合材料的非等温结晶动力学

2.2.1 Ozawa方程分析 Ozawa基于Evans理论,从高聚物结晶的成核和生长过程出发,推导出等速升温或等速降温时的结晶动力学方程[15]:

1-X(T)=exp[-F(T)/Φm]

式中, X( T)为在温度 T时的相对结晶度, Φ为升温或降温速率, m是Ozawa指数, F( T)与成核方式、成核速率、晶核的生长速率等因素有关,是温度的函数。 其线性形式为:

ln{-ln[1-X(T)]}=lnF(T)-mlnΦ

以ln {-ln [1- X( T)]}对ln Φ作图,拟合直线的斜率为- m,截距为ln F( T)。图2为一定温度下WPU和WPU/1.0%FGNs复合材料的ln {-ln [1- X( T)]}- ln Φ图。 从图2可以看出,Ozawa方程能很好的拟合WPU非等温结晶过程,所得的参数列于表2。 从表2可知,随着温度的降低,ln F( T)值有增大的趋势。 等速降温过程中,高温阶段的WPU分子链运动剧烈,形成的晶核比较容易被破坏,此时低成核速率决定了结晶总速率很小。 随着温度逐渐降低,WPU分子链运动减弱,成核速率增大,链段向晶核扩散和规整堆积,结晶总速率提高,表现为ln F( T)的值的增加。 由于Ozawa方程并未考虑到Avrami指数 m与温度之间的关系,故而Ozawa方程求得的Ozawa指数并无法表征聚合物的结晶方式,但可以通过 m的变化来定性描述结晶方式的变化情况。 比较各样品的 m值可以发现,WPU/FGNs的 m值比WPU大,这表明FGNs的加入导致WPU的结晶维数增加。

图2 Ozawa方程处理WPU( A)和WPU/1.0%FGNs( B)复合材料非等温结晶过程的ln {-ln [1- X( T)]}- ln Φ拟合直线图Fig.2 Ozawa plots of ln {-ln [1- X( T)]} versus ln Φ for non-isothermal crystallization of WPU( A) and WPU/1.0%FGNs( B) composites

表2 Ozawa方程处理WPU和WPU/FGNs非等温结晶过程的动力学参数 Table 2 Kinetic parameters for non-isothermal crystallization of WPU and WPU/FGNs composites based on Ozawa equation

2.2.2 莫志深方程 处理高聚物静态等温结晶过程最常用的是Avrami方程[16]。 Avrami方程是联系相对结晶度 X( t)和时间 t的数学方程,Ozawa方程是联系 F( T)和 Φ的数学方程。 基于式(2)中 t与 T的关系,莫志深[17]将Avrami方程和Ozawa方程结合,得到如下方程式:

lgϕ=lgP(T)-algt

式中, P( T) =[ F( T) /Z]1 /m, a=n/m。 莫志深方程克服了Ozawa方程和Avrami方程的缺点,而且得到的非等温动力学参数 P( T)具有明确意义[17]。 P( T)的物理意义为对某一聚合物结晶体系在单位时间内,要达到某一结晶度必须选取的冷却速率值。 P( T)可以用来衡量结晶速率的快慢, P( T)越大,体系的结晶速率越低。 以lg Φ对lg t作图,拟合直线的斜率为- a,截距为lg P( T)。图3为一定温度下WPU和WPU/1.0%FGNs的lg Φ-lg t图。 从图3可以看出,lg Φ和lg t之间线性关系良好,说明莫志深方程处理聚氨酯非等温结晶过程是可行的。 所得的参数列于表3。 从表3可以看出,随着相对结晶度的增大, P( T)值不断增大。 这表明在单位时间内,各样品结晶要达到高的相对结晶度要选取高的冷却速率。 当 X( t)相同时,WPU/FGNs的 P( T)值均大于WPU,说明FGNs为1.0%以下时,WPU/FGNs结晶速率比纯WPU快。 对于WPU/FGNs,FGNs增加至0.3%, P( T)值逐渐减小,继续增加FGNs至1.0%, P( T)值又逐渐增大。 这表明随着FGNs的增加,WPU/FGNs结晶速率先增大后减小。 这是由于低质量分数的FGNs起到异相成核剂的作用,促进了结晶过程的进行。 而高质量分数FGNs的存在可能导致FGNs片层减缓了WPU链段向晶核扩散和规整堆积的速度,造成晶粒生长的缓慢,总结晶速率减小,也可能是FGNs过多而团聚,进而削弱了其成核剂的作用。

图3 Mo方程处理WPU( A)和WPU/1.0%FGNs( B)复合材料非等温结晶过程的lg Φ-lg t拟合直线图Fig.3 Mo plots of lg Φ versus lg t for non-isothermal crystallization of WPU( A) and WPU/1.0%FGNs( B) composites

表3 Mo方程处理WPU和WPU/FGNs复合材料非等温结晶过程的动力学参数 Table 3 Kinetic parameters for non-isothermal crystallization of WPU and WPU/FGNs composites based on Mo equation
2.3 WPU/FGNs纳米复合材料的非等温结晶活化能

考虑到非等温结晶过程不同冷却速率对DSC曲线的影响,聚合物结晶活化能可以用Kissinger方程[18]计算:

d(lnΦT2p)d(1Tp)=-ΔER

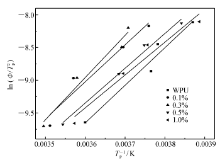式中, Φ为降温速率,Δ E为总活化能, Tp为峰温值。 根据表1中的数据,以ln ( Φ/ T2p)对1/ Tp作图,如图4所示。 通过拟合直线可以求得各个样品的Δ E值,列于表4。

图4 WPU和WPU/FGNs纳米复合材料的ln ( Φ/ T2p)-1/ Tp拟合直线图Fig.4 Linear fit to ln ( Φ/ T2p)-1/ Tp curves of WPU and WPU/FGNs composites

从表4中可以看出,相比于WPU,增加FGNs至0.3%,复合材料活化能显著降低。 继续增加FGNs至1.0%,复合材料活化能持续增加,且高于WPU活化能值。 结晶活化能分为成核活化能和转移活化能。 成核活化能指一定尺寸的晶核形成所需的自由能,转移活化能指分子链段穿过相界面到达晶核表面所需的活化能[19]。 FGNs作为成核剂,降低了成核活化能,同时其片状结构阻碍了链段向晶核的移动,提高了转移活化能。 FGNs质量分数的不同决定了两种因素何种占主导地位,进而导致了复合材料活化能的变化。

表4 Kissinger方程处理WPU和WPU/FGNS复合材料非等温结晶过程所得活化能值 Table 4 Effective activation energy of WPU and WPU/FGNs composites in the process of non-isothermal crystallization based on Kissinger equation
3 结 论

在水溶性聚氨酯/功能化石墨烯(WPU/FGNs)纳米复合材料的非等温结晶过程中,FGNs起到异相成核剂的作用,提高了WPU的结晶起始温度、峰值温度和结晶速率。 Ozawa方程和莫志深方程适用于研究WPU/FGNs纳米复合材料的非等温结晶动力学。 动力学数据表明,随着温度的降低,WPU结晶速率提高;FGNs的加入加速了WPU的结晶过程,改变了WPU的成核机理;随着FGNs质量分数的增加,WPU/FGNs结晶速率先增大后减小。 FGNs质量分数为0.3%时,WPU/FGNs的结晶活化能低于WPU;FGNs质量分数为0.5%和1.0%时,WPU/FGNs的结晶活化能高于WPU。

参考文献
[1] Lee C G, Wei X D, Kysar J W, et al. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene[J]. Science, 2008, 321(5887): 385-388. [本文引用:1]
[2] Nair R R, Blake P, Grigorenko A N, et al. Fine Structure Constant Defines Visual Transparency of Graphene[J]. Science, 2008, 320(5881): 1308-1308. [本文引用:1]
[3] Novoselov K S A, Geim A K, Morozov S V, et al. Two-dimensional Gas of Massless Dirac Fermions in Graphene[J]. Nature, 2005, 438(7065): 197-200. [本文引用:1]
[4] Balandin A A, Ghosh S, Bao W Z, et al. Superior Thermal Conductivity of Single-layer Graphene[J]. Nano Lett, 2008, 8(3): 902-907. [本文引用:1]
[5] Stoller M D, Park S, Zhu Y W, et al. Graphene-based Ultracapacitors[J]. Nano Lett, 2008, 8(10): 3498-3502. [本文引用:1]
[6] Singh V, Joung D, Zhai L, et al. Graphene Based Materials: Past, Present and Future[J]. Prog Mater Sci, 2011, (56): 1178-1271. [本文引用:1]
[7] Leblanc J L. Rubber filler Interactions and Rheological Properties in Filled Compounds[J]. Prog Polym Sci, 2002, 27(4): 627-687. [本文引用:1]
[8] Luo X M, Zhang, Ren J, et al. Preparation and Properties of Functionalized Graphene/waterborne Polyurethane Composites with Highly Hydrophobic[J]. J Appl Polym Sci, 2015, 132(23): DOI: 10.1002/APP.42005. [本文引用:1]
[9] Pokharel P, Lee D S. Thermal and Mechanical Properties of Reduced Graphene Oxide/Polyurethane Nanocomposite[J]. J Nanosci Nanotechnol, 2014, 14(8): 5718-5721. [本文引用:1]
[10] Donath F A. Experimental Study of Shear Failure in Anisotropic Rocks[J]. Geol Soc Am Bull, 1961, 72(6): 985-989. [本文引用:1]
[11] Begenir A, Michielsen S, Pourdeyhimi B. Melt-blowing Thermoplastic Polyurethane and Polyether-block-amide Elastomers: Effect of Processing Conditions and Crystallization on Web Properties[J]. Polym Eng Sci, 2009, 49(7): 1340-1349. [本文引用:1]
[12] Shehzad F, Thomas S P, Al-Harthi M A. Non-isothermal Crystallization Kinetics of High Density Polyethylene/graphene Nanocomposites Prepared by In-situ Polymerization[J]. Thermochim Acta, 2014, 589: 226-234. [本文引用:1]
[13] Yang Z P, Lu H B. Nonisothermal Crystallization Behaviors of Poly(3-hexylthiophene)/reduced Graphene Oxide Nanocomposites[J]. J Appl Polym Sci, 2013, 128(1): 802-810. [本文引用:1]
[14] Hummers Jr W S, Offeman R E. Preparation of Graphitic Oxide[J]. J Am Chem Soc, 1958, 80(6): 1339. [本文引用:1]
[15] Ozawa T. Kinetics of Non-isothermal Crystallization[J]. Polymer, 1971, 12(3): 150-158. [本文引用:1]
[16] Avrami M. Kinetics of Phase Change. Ⅰ General Theory[J]. J Chem Phys, 1939, 7(12): 1103-1112. [本文引用:1]
[17] MO Zhishen. A Method for the Non-isothermal Crystallization Kinetics of Polymers[J]. Acta Polym Sin, 2008, (7): 656-661(in Chinese).
莫志深. 一种研究聚合物非等温结晶动力学的方法[J]. 高分子学报, 2008, (7): 656-661. [本文引用:2]
[18] Kissinger H E. Variation of Peak Temperature with Heating Rate in Differential Thermal Analysis[J]. J Res Nat Bur Stand, 1956, 57(4): 217-221. [本文引用:1]
[19] Zhang F, Peng X C, Yan W B. Nonisothermal Crystallization Kinetics of In Situ Nylon 6/Graphene Composites by Differential Scanning Calorimetry[J]. J Polym Sci Part B: Polym Phys, 2011, 49(19): 1381-1388. [本文引用:1]